Moti dei pianeti
Il Sistema Solare
I principali moti dei pianeti sono "rotazione" e "rivoluzione". Vi sono poi altri moti percepibili in tempi astronomici lunghi che per questo vengono definiti millenari come "precessione" e "nutazione" di cui parleremo in un altra sezione.
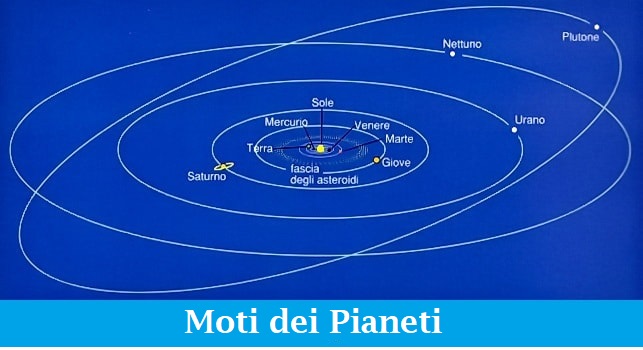 E' noto che tutti i pianeti ruotano attorno al sole seguendo delle orbite ellittiche (quasi circolari) e più o meno angolate rispetto al piano equatoriale del Sole.
E' noto che tutti i pianeti ruotano attorno al sole seguendo delle orbite ellittiche (quasi circolari) e più o meno angolate rispetto al piano equatoriale del Sole.
Oltre a questo moto detto di “rivoluzione”, tutti i pianeti ruotano anche su se stessi o meglio attorno al proprio asse polare. Questo moto viene definito “rotazione”.
All’inizio della storia del Sistema Solare ogni pianeta probabilmente avrà avuto il proprio periodo di rotazione determinato da condizioni iniziali che purtroppo non sono note. Secondo le teorie più accreditate i pianeti si sarebbero formati per aggregazione gravitazionale di diversi materiali (polveri e gas) presenti, in grandi quantità, nello spazio cosmico. In questo contesto un fattore rilevante, che ha influenzato inizialmente la rotazione dei pianeti, è stato il fenomeno di "conservazione del momento angolare" che ha inciso nella fase in cui si sono aggregati i singoli corpi (planetesimi) che hanno composto il pianeta finale (per esempio: si pensi ad una ballerina che ruota lentamente con corpo e braccia distesi e che accelera la rotazione comprimendo corpo e braccia).
Con il passare del tempo però i periodi di rotazione possono cambiare e ciò a causa di collisioni o/e interazioni gravitazionali tra corpi celesti come stelle, satelliti naturali, pianeti ed altri ancora.
Le leggi fisiche che regolano il moto di rivoluzione dei pianeti sono note con il nome di “Leggi di Keplero” dal famoso astronomo tedesco Johannes von Kepler (in italiano: Giovanni Keplero) che le scrisse agli inizi del 1600.
Esse sono valide solo se sono soddisfatte le seguenti condizioni:
- la massa del pianeta deve essere trascurabile rispetto a quella della stella di riferimento;
- Le interazioni gravitazionali tra diversi pianeti devono essere trascurabili. Esse infatti portano a leggere perturbazioni sulla forma delle orbite).
Nel nostro Sistema Solare tali condizioni sono approssimativamente soddisfatte e probabilmente questo vale anche per molti altri sistemi stellari. Le cose si complicano per i sistemi stellari multipli ( es. sistemi binari, ternari ecc.) dove bisogna ricorrere ad altri tipi di calcolo.
| Prima legge di Keplero |
|---|
| “L’orbita di un pianeta è un’ellisse, di cui il sole occupa uno dei due fuochi”. |
Questa importante scoperta diede una nuova spinta verso l' astronomia moderna perfezionando la "rivoluzionaria" teoria eliocentrica di Copernico(inizio XVI secolo) ed affossando definitivamente il modello geocentrico di Aristotele e Tolomeo.
Le orbite dei pianeti che ruotano attorno al sole non sono dunque dei "perfetti" cerchi, bensì delle ellissi.
conoscendo quindi le proprietà delle ellissi è stato possibile calcolare, con estrema precisione, i parametri orbitali di tutti i corpi celesti che ruotano attorno al Sole
L’ellisse è una figura piana definita dalla seguente proprietà: la somma delle distanze, da qualsiasi punto perimetrale dell’ellisse, da due punti fissi (detti fuochi dell’ellisse) è sempre costante.
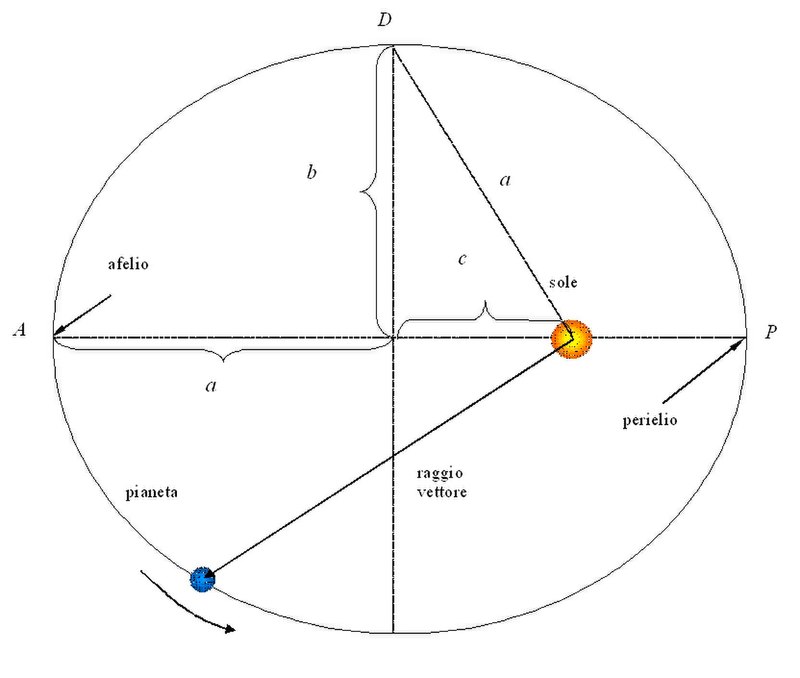
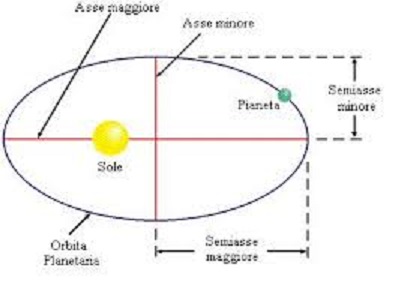
Nella figura a fianco è rappresentata un'orbita ellittica, con indicati i suoi parametri caratteristici: semiasse maggiore (a), semiasse minore (b), semi-distanza focale (c), eccentricità (e).
Tra questi parametri esistono le relazioni seguenti:
c = √ (a-b)
e = eccentricità = c/a
Con il valore di "e" che va da ≤ 0 a < 1
Con e = 1 si ha una parabola mentre con e > 1 si ha una iperbole.
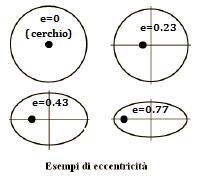
Come si vede dalla figura a lato, l' ellisse risultà essere sempre più allungata al crescere dell' eccentricita mentre con eccentricità=0 si ha un cerchio.
La prima e più importante conseguenza della prima legge di Keplero riguarda il fatto che ognuno dei pianeti del Sistema solare,
nel corso del proprio moto di rivoluzione, si troverà più vicino al Sole in alcuni punti mentre in altri sarà più lontano.
Più precisamente le distanze dei pianeti dal Sole variano continuamente nel corso dei rispettivi moti di rivoluzione,
e per ciascuna orbita ci sono due particolari punti che realizzano la massima e la minima distanza dal Sole,
detti rispettivamente Afelio e Perielio.
Per esempio, la Terra raggiunge il punto più vicino al Sole (perielio) attorno al 2 Gennaio (quando nell'emisfero nord è inverno!)
a una distanza di 147 000 000 di Km e il punto più lontano (afelio) attorno al 5 di Giugno, a una distanza di 152 000 000 di chilometri.
| Seconda legge di Keplero |
|---|
| “Il raggio vettore del pianeta descrive aree uguali in tempi uguali”. |

Quindi la velocità orbitale dei pianeti non è costante, ma varia lungo i vari punti dell'orbita.
Le due aree, evidenziate nella figura a lato, sono infatti uguali e quindi vengono percorse nello stesso tempo. Ne deriva che in prossimità del perielio, dove il raggio vettore è più corto e l'arco di ellisse corrispondente (C-D) più lungo, la velocità orbitale è maggiore mentre all'afelio dove il raggio vettore è più lungo e l'arco di ellisse corrispondente (A-B) più corto, la velocità orbitale è minore.
In sostansa il pianeta ha una velocità orbitale maggiore quanto più si avvicina al Sole e minure quanto più se ne allontana. Al perielio la velocità sarà massima mentre all' afelio sarà minima.
La velocità angoare della Terra, ad esempio, varia da un massimo di 30,2865 Km/s (al perielio) ad un minimo di 29,2911 Km/s (all’ afelio). La sua velocità media risulta di 29,78 km/s e compie, in un anno, circa 940 milioni di Km.
| Tersa legge di Keplero |
|---|
| “I quadrati dei periodi di rivoluzione sono direttamente proporzionali ai cubi dei semiassi maggiori delle loro orbite”. |
La terza legge di Kepleromette in relazione le distanze dei pianeti dal Solecon le rispettive durate di un’orbita completa.
In particolare afferma che rapporto tra il quadrato del periodo di rivoluzione (P) e il cubo del semiasse maggiore dell'orbita (R) è lo stesso per tutti i pianeti. Abbiamo quindi :
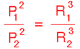
In sostanza il periodo di rivoluzione di un pianeta cresce esponenzialmente con l’ aumentare della sua distanza dal Sole.
Infatti ad esempio Mercurio (il pianeta più vicino al Sole) ha un periodo di rivoluzione di 87,969 giorni mentre Nettuno (il pianeta più lontano al Sole) ha un periodo di rivoluzione di 60.189 giorni.
Conoscendo il tempo di rivoluzione di un pianeta, la terza legge di Keplero consente di ricavarne immediatamente la distanza media dal Sole prendendo come unità la distanza Terra-Sole = 149.600.000 Km detta anche Unità Astronomica (UA). Ad esempio, Saturno compie una rivoluzione attorno al Sole in29,46 anni: la sua distanza media vale ³√29,46 ² = 9,54. Quindi Saturno mediamente dista dal sole 9,54 volte più della distanza Terra-Sole ovvero 9,54 UA.
Orbite e velocità di fuga
La forza di gravità con cui due corpi celesti si attraggono fu formulata da Isaac Newton nel 1687. Essa è direttamente proporzionale al prodotto delle due masse e inversamente proporzionale al quadrato delle loro distanze
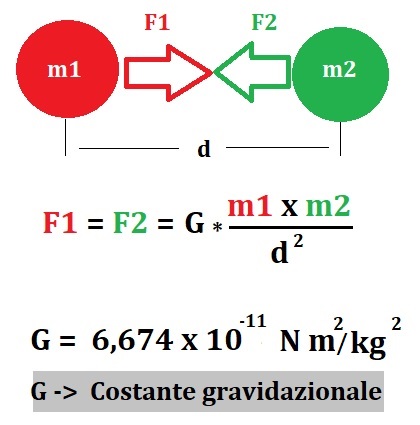 Nel Sistema Solare il Sole possiede il 99% della massa totale e ciò rende approssimativamente trascurabile le masse dei corpi celesti che vi orbitano attorno.
Ne deriva che Il tipo di orbita che un corpo celeste (pianeta, asteroide, cometa ecc.) compie attorno al Sole, dipende essenzialmente dalla velocità orbitale del corpo celeste e dalla distanza che lo separa dal Sole.
Nel Sistema Solare il Sole possiede il 99% della massa totale e ciò rende approssimativamente trascurabile le masse dei corpi celesti che vi orbitano attorno.
Ne deriva che Il tipo di orbita che un corpo celeste (pianeta, asteroide, cometa ecc.) compie attorno al Sole, dipende essenzialmente dalla velocità orbitale del corpo celeste e dalla distanza che lo separa dal Sole.
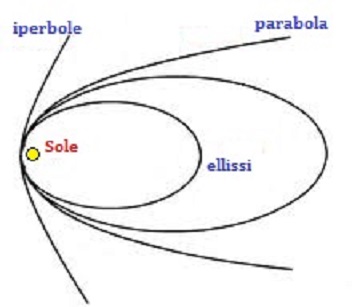 Alla distanza della Terra , un corpo di massa trascurabile segue una orbita ellittica se ha una velocità inferiore a 42 Km/s (infatti la velocità orbitale della terra e di circa 30 Km/s); se la velocità raggiunge 42 Km/s allora l’ orbita diventa parabolica e il corpo si allontana all’ infinito; se supera questo valore il corpo va verso l’ infinito su una orbita iperbolica.
Alla distanza della Terra , un corpo di massa trascurabile segue una orbita ellittica se ha una velocità inferiore a 42 Km/s (infatti la velocità orbitale della terra e di circa 30 Km/s); se la velocità raggiunge 42 Km/s allora l’ orbita diventa parabolica e il corpo si allontana all’ infinito; se supera questo valore il corpo va verso l’ infinito su una orbita iperbolica.
Il valore di 42 Km/s è quindi la velocità minima che deve possedere un corpo, che si trova alla stessa distanza della Terra dal Sole, per “fuggire” dal sistema solare. Questa velocità viene definita come velocità di fuga e diminuisce al crescere della distanza. Alla distanza di 1 milione di Km dal centro del Sole la velocità di fuga è di 500 km/s mentre alla distanza di Giove, che è di 780 milioni di Km , la velocità di fuga è di 18,4 Km/s.
Il concetto di velocità di fuga ovviamente non riguarda solo il Sole ma si può estendere a tutti i corpi celesti legati tra di loro da interazioni gravitazionali. Ad esempio per sfuggire al campo gravitazionale terrestre un corpo deve avere una velocità di fuga di 11,2 Km/s.
Un corpo al quale viene impressa questa velocità può “fuggire” dal campo gravitazionale terrestre ma se non supera i 42 Km/s resta sempre vincolato all’ interno del sistema solare. Analogamente a quanto già detto, al crescere della distanza dal suolo terrestre cioè a 3600 km di quota (10.000 Km dal centro) la velocità di fuga si riduce a 8,9 Km/s.
Per calcolare la velocità di fuga, di un corpo di massa trascurabile, da un corpo celeste di massa M ci si avvale della:
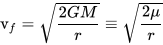
dove:
- M : è la massa del pianeta
- G : è la costante gravitazionale;
- r : è il raggio del pianeta;
- μ = GM : è nota, in campo aerospaziale, come costante gravitazionale planetaria.
La velocità di fuga assume particolare importanza in campo aereo-spaziale dove occorre calcolare, di volta in volta e con estrema precisione, le spinte necessarie per portare un “vettore” a percorrere determinate orbite attorno alla Terra o al di fuori del campo gravitazionale terreste.
Configurazioni planetarie
La distanza e la visibilità dei pianeti dalla Terra variano continuamente a causa del loro moto di rivoluzione e a quello della Terra.
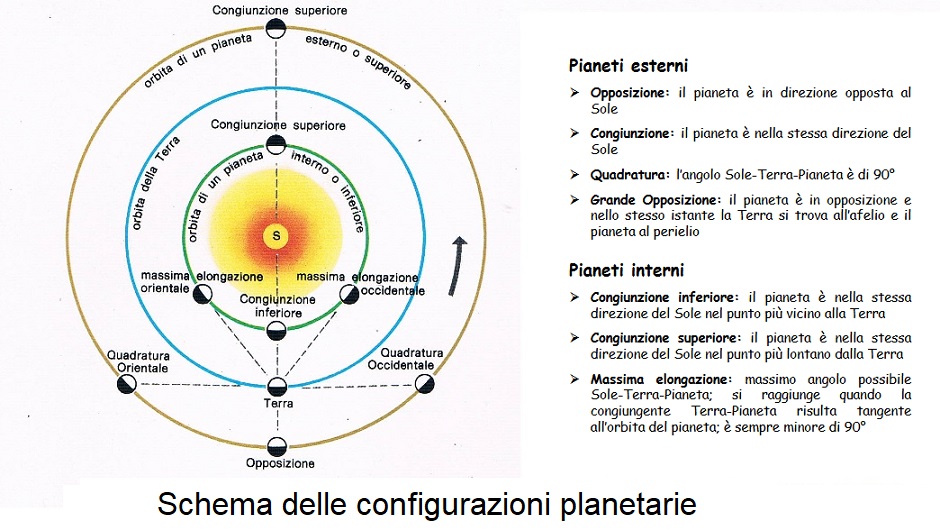 Quando un pianeta appare in direzione opposta a quella del Sole si dice in opposizione ed allora si trova alla minima distanza da noi.
Quando un pianeta appare in direzione opposta a quella del Sole si dice in opposizione ed allora si trova alla minima distanza da noi.
Quando invece si trova nella medesima direzione del Sole si dice in congiunzione ed è inosservabile perché la luce solare ne impedisce la visione.
I pianeti che gravitano su orbite interne a quella della Terra ( i cosiddetti pianeti interni: Venere e Mercurio ) non possono evidentemente trovarsi mai in opposizione.
Si possono invece trovare in congiunzione sia essendo al di là che al di qua del Sole: nel primo caso la congiunzione si dice superiore, nel secondo inferiore.
Venere e Mercurio non possono apparire mai più lontani di un dato angolo dal Sole (28° per Mercurio e 48° per Venere) e quando raggiungono questa massima distanza angolare si dice che si trovano alla massima elongazione.
Un pianeta si dice in quadratura quando si vede in una direzione che fa un angolo retto con la direzione in cui si vede il Sole. È evidente che i pianeti interni non possono mai trovarsi in quadratura.
Le opposizioni, le congiunzioni, le quadrature e le massime elongazioni sono posizioni caratteristiche delle cosiddette configurazioni planetarie.
Al verificarsi delle opposizioni si hanno le migliori condizioni per l'osservazione dei pianeti esterni; e ciò sia per la minima distanza sia, per la favorevole posizione in cielo.
Data l'eccentricità delle orbite la distanza non è però la medesima per tutte le opposizioni: la differenza da un'opposizione all'altra è particolarmente sensibile per Marte la cui orbita è fra le più eccentriche fra quelle planetarie.
Nelle opposizioni che si verificano quando Marte è all'afelio, la distanza del pianeta dalla Terra è di 99 milioni di chilometri, in quelle che si verificano quando invece è al perielio, la distanza è di soli 56 milioni di chilometri. Le opposizioni che avvengono quando Marte è in prossimità del perielio, e che vengono dette grandi opposizioni, sono le occasioni più favorevoli per l'osservazione di Marte. Fu nella grande opposizione del 1877 che l’ astronomo italiano Schiaparelli vide per la prima volta i famosi canali.
